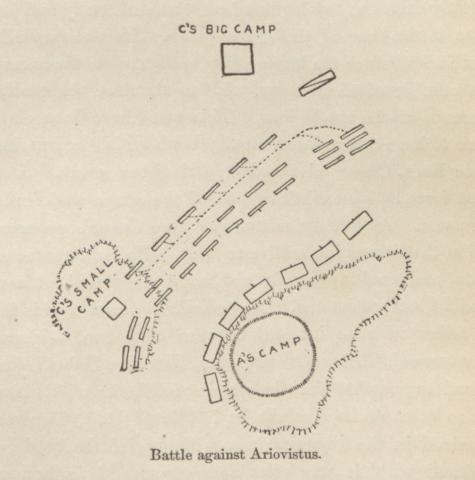
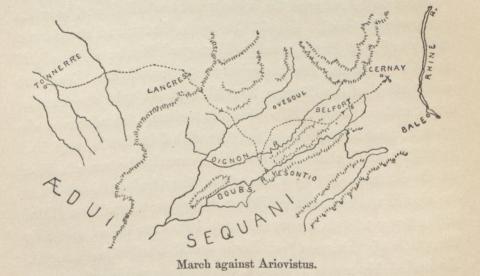
quaestor, -ōris m.: quaestor.
praeficiō, -ficere, -fēcī, -fectus : set over, put in command of.
quod : conj., that, in that, because, since; as to the fact that: the fact that.
fīrmus, -a, -um: strong, powerful; stable, firm, steady; trustworthy.
animadvertō, -vertere, -vertī, -versus : turn the thoughts toward, give attention to, notice, perceive; animadvertere in, take notice of, take measures against, punish; cf. animum advertere.
nostri -orum m. pl.: our men
ācriter : adv., sharply, keenly, fiercely; vigorously, courageously; sup, ācerrimē.
repente : adv., suddenly, unexpectedly.
prōcurrō, -currere, -cucurrī or -currī, -cursus : run forward, rush forward, charge.
pīlum, -ī, n.: javelin; mūrāle pīlum, wall-javelin, a heavy javelin to be hurled from fortifications.
coniciō, -icere, -iēcī, -iectus : throw together; throw, hurl; station, put; attribute; in fugam conicere, put to flight, rout; sē conicere, dash, rush.
comminus : adv., hand to hand, at close quarters.
Germānus, -ī, m. : a German; pl., the Germans; as adj., Germānus, -a, -um, German
phalanx, -angis, f.: phalanx, a compact body of troops in battle array.
complūrēs, -a or -ia : pl. adj., many, several.
īnsiliō, -silīre, -siluī : leap against, leap.
scūtum, -ī, n.: shield.
revellō, -vellere, -vellī, -vulsus : pull away, tear away, tear out.
dēsuper : adv., from above.
vulnerō, -āre, -āvī, -ātus : wound.
sinister, -tra, -trum: left, on the left; as subst., f. (sc. manus), left hand.
vehementer : adv., furiously, eagerly, vigorously; greatly, extremely, exceedingly.
Publius -iī m.: Publius (name) abbreviated "P."
Crassus, -ī, m.: Crassus, a Roman cognomen: (1) Marcus Licinius Crassus, the triumvir, consul in 55 b.c. See Introd., p. 11. (2) Marcus Licinius Crassus, son of (1). He was quaestor with Caesar. (3) Publius Licinius Crassus, a younger son of (1). He was one of Caesar's officers.
adulēscēns, -entis : adj., young; as subst., m. and f., young man, young woman; often with proper names, the younger, to distinguish from older persons of the same name.
equitātus, -ūs m.: cavalry, body of horsemen.
praesum, -esse, -fuī : be before, be set over, be in command of.
expedītus, -a, -um : unencumbered, lightly equipped, without luggage; free, unembarrassed, easy.
versor, -ārī, -ātus : move about; busy oneself, be engaged, be busy; live, dwell, exist; be.
subsidium, -ī n.: support, aid; protection; provision; troops in reserve, reserve; auxiliary troops.